What Can Circuitboards Teach Us About Life?
How does electricity flowing through circuits turn into a “living” computer?
This newsletter is my attempt to capture and share some of what I'm learning as I study AI, technology, and science. If you know someone who might find it fun, please forward it along.
Warning: This month is about to get very nerdy. I wanted to try out a different style, more focused on going deep into one big thing I’m thinking about. I’d love your feedback on whether you prefer this or the past style that’s a little lighter.What is Life?
Since reading The Demon in the Machine, I’ve been spending a lot of time thinking about what it means for something to be alive.
Life is weird as hell, and we just take it for granted. We all assume that living organisms have goals, motivations, etc, and that atoms and molecules blindly follow physical laws. But biological systems are physical systems. Somehow the former has to come out of the latter.
I won’t try to summarize the book, but the author’s thesis is that life is information. Information alone is enough to locally reverse entropy (this PBS video gives a good summary of how), and that allows life to create circumstances that would be impossible to “naturally” happen in a pure physical system (for example, shooting a rocket into space).
The argument is a good one, but it got me wondering: How does information turn into life?
Imagine I wrote your complete DNA sequence on a strip of paper. That would encode the same information as your genome, but it wouldn’t just magically spring to life. What’s the difference?
I couldn’t find an answer I could get my head around in the bio literature, but it led me to try to understand by looking at a parallel question: How does electricity flowing through wires turn into a “living” computer?
How Does a Computer Come Alive?
Computers may not literally be alive, but they definitely have a similar kind of magic. Somehow, a mix of chips (static wiring circuits) and information (static encoded states) are able to combine to create something that “comes alive” to be able to do things.
The more I thought about it, the less sense it made.
I’d read about Universal Turing Machines, so I understood the basic principle of how a general computer could exist to solve any problem: the idea is that, if you have a tape of 1s and 0s, and a reader that can examine the tape, follow a set of rules, and edit the tape, it can theoretically do any computation that any computer could do.
But this felt unsatisfying (at least, based on my limited understanding). Where did the reader get this set of rules? How did it understand them? How did it even know it was supposed to be moving in the first place?
I finally found my answer in a course called NAND2Tetris.
From NAND to Addition
Let’s start from the most simple, boring system possible and build up from there.
Imagine you have an electrical circuit with an input, an output, and two gates in series. If both gates are closed and you shoot electricity in, it’ll come out the other end. If either gate is open, then the electricity won’t come out. In other words, we can shoot electricity in, and the output will tell us whether the first AND second gate are closed.
In a sense, this circuit can answer logical questions. Say you have the logical statement “If it is raining out, and it is cold out, I will stay inside.” You can encode the first gate to close when it is raining, and the second to close when it is cold. Now your circuit answers the question “Will I stay inside?” If both gates are closed, current flows out. Otherwise, it doesn’t.
This is an AND gate. But another simple (and more useful) building block is something called a NAND Gate. This is the opposite of the circuit above, where the current flows out unless both gates are closed. The magic of the NAND gate is that, from this simple building block, we can build up more and more complex logic, allowing the gate to “answer” more and more complex questions:
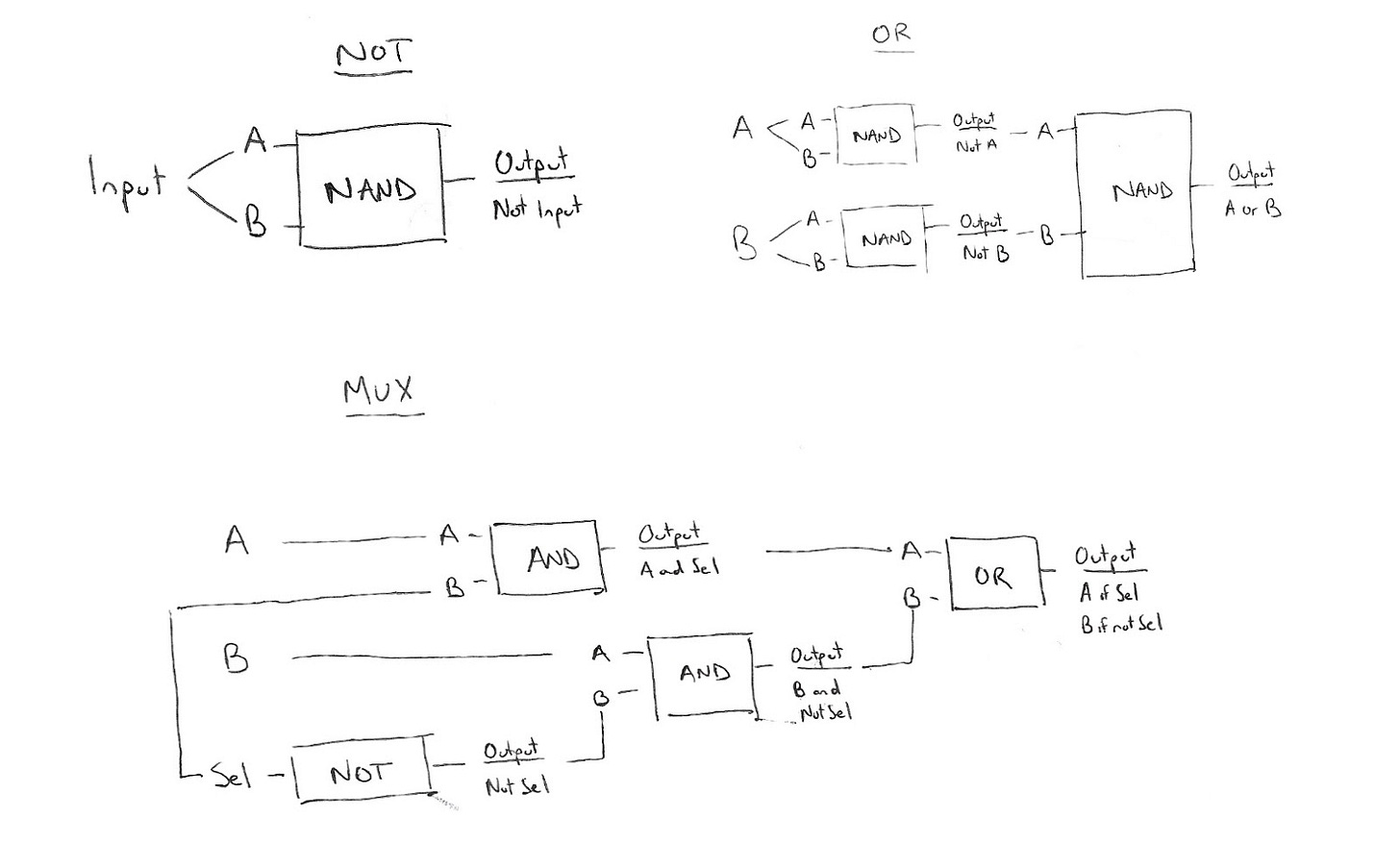
So far, these gates are just answering “yes or no” questions for us, but things can get more complex quickly. We can use the inputs to represent binary digits, and then wire things up in such a way that we two inputs can “merge” into a set of outputs that represent the binary value of adding them together.
This is the first step that really felt magical to me. We went from just having an electrical circuit, to having it wired to give the yes / no answers to logical questions about the inputs, to all of a sudden being able to add numbers togethers.
From addition, it’s relatively easy to add other computations. The result is a chip called the Arithmetic Logic Unit, or ALU.
From Addition to a Computer
We now have an adding machine, just made out of electricity. For most of human history, that would be pretty fucking mindblowing. But it’s not a computer.
To take the next step, we need a code, a way to tell the adding machine what actions to perform, what values to store, and what to do next. With 16 inputs, we can encode for over 65,000 possible instructions (here’s a quick primer on binary), which is enough for everything we need. We can simply route these inputs to the different chips we’ve already built, and use those inputs to lead to addiction or subtraction, store values in memory or retrieving from memory, and everything else needed to make our computer “Turing Complete”.
But where do the instructions come from? Eventually we’d want programmer to be able to write them, but to start, we can pre-load them in a separate section of memory called the ROM (read-only memory). After each action the CPU takes, something called the Program Counter outputs the address of the next action. This address goes to the ROM, and the ROM sends back the specific instruction code from that line of the instructions, which tells the CPU what to do next.
Let’s look at how info actually flows:
When someone pushes the “on” button of our computer, the Program Counter is triggered to send out the value 1.
The output of the Program Counter goes to the ROM, which translates an input (address) for an output (the instructions it has stored in that address). As a result, it outputs the first 16 bit instruction.
That instruction goes to the CPU. Instructions can be to add numbers, store numbers in temporary storage, jump to another part of the program, etc.
The CPU performs that action (according to instructions), and the Program Counter sends which instruction to perform next to the ROM.
The ROM sends back the next instruction, and the cycle continues.
From a quick explanation, it may be hard to imagine how these limited instructions can do all the things a computer can do. But with the ability to store 16 bit numbers, perform math on them, and conditionally jump to different parts of the program, we can do anything. The rest of computer science is writing abstractions on top of this so that programmers can write in convenient language rather than 16 digit lines of 1s and 0s.
From a Computer to Life?
So, finally, let’s get back to the real question: How does this relate to life?
It’s easy to see the parallels between ROM and DNA. They both encode the instructions, but they need a system around them to use those instructions. It needs “life breathed into it” in some way.
The question I started the course with was “How does a computer know what those instructions mean and what it even means to execute them, when you can’t use the language of the instructions to tell it?”
The answer I ended with is that the language the computer understands is built into its wiring.
If I decided on a different code for 16 bit instructions, I would just need to wire up the chips differently and it would work fine. The 16 bit instructions themselves don't have any meaning. It’s the wiring that turns the gibberish of 1s and 0s into “information” that actually encodes something meaningful. And it’s the wiring that allows the pushing of the “on” button to trigger the beginning of executing those instructions.
What’s the biological parallel? In adult cells, it’s the series of enzymes that transcribe DNA into mRNA, and ribosomes and tRNA that translate those into proteins. The chemical soup is the “wiring” that turns a meaningless molecule like DNA into something that encodes information. Without that wiring, the patterns in DNA wouldn’t mean any more than the same pattern written on a piece of paper.
This feels mostly satisfying. It makes sense that DNA gets its meaning through the specific machinery of the cell, and it’s that magical chemical context that brings this innate molecule to life.
But it opens up other questions that I still don’t have the answers to:
How does this process start in a zygote? Egg cells come preloaded with mitochondria. Do they already have the rest of these enzymes? If not, how do they create them? After all, it would be impossible for a computer to start with the ROM and no ability to read it, and create its own wiring from that.
How do the conditionals work? Computers are very concrete in their reading of the program. When the Program Counter says “jump to instruction 200”, all the rest of the instructions are ignored. Cells are much more driven by equilibria — performing all instructions at once, and methylating DNA or neutralizing histones to get genes read more or less. How does a system like that succeed in creating such differentiated and unique cells, and succeed so consistently?
So… lots more to learn :)
Until next month,
Zach

